| 学习数学的目的是为了应用数学知识解决问题,而函数的应用题是一种应用广泛、实用性又极强的问题,因此建立函数模型解决应用问题是高考的热点题型之一.在解此类问题时,要充分应用函数知识.
函数模型问题,就是指用数学的方法将一个表面上非数学问题或非完全的数学问题转化成函数应用问题,分析和解答函数应用问题的思维过程为:
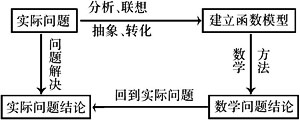
上图表中的第一步:“实际问题”经分析、联想、抽象、转化为“建立函数模型”,这一步应从审题开始,通过分析找出题设与结论的数学关系,进一步转化为函数,即建立合理的数学模型,因此,这一步称之为数学化;第二步:“函数模型”经过数学方法的处理,得到数学问题结论,这一步就是采用数学的方法,解决函数模型所表述的数学问题,因此,这一步称之为数学解决;第三步是:“数学问题结论”,这一步就是将数学结论转化为实际问题的结论,因此,这一步称之为实际化;最后一步是对实际问题的结论作出解答.
应用数学知识解函数模型问题的方法步骤:
(1)解读:通过阅读题目,了解实际背景、收集各种数据.要弄清题目中的每一个词语,特别是以前从未见过的术语,要认真琢磨其含义,对于一些常见的关键性语句,要领会其数学意义,注意挖掘隐含因素.然后将题目中生活、生产中的语言准确地用数学语言表达出来;正确地将实际问题转化为函数模型,这是解题的关键,转化来源于对已知条件的综合分析、归纳和抽象,并与熟知的函数模型相比较,以确定函数模型的种类.
(2)建模:根据题目要求,分清条件和结论,理顺题目中各种数量之间的关系,联想归结为自己所熟悉的某种基本数学关系,如:总价 = 单价 × 件数,利润 = 售价 - 成本等等.联想与题目有关的数学知识和数学方法,并注意对变量的限制条件;再用相关的函数知识,进行合理设计,确定最佳解题方案,进行数学上的计算求解.
(3)解模:函数应用题中建立的数学模型,大都为一种符号模型,也就是把题目中的已知量、未知量、常量、变量、参变量等分门别类的列出,再摆出题目的各种约束条件.对这种数学框架用数学方法处理,得到数学结论.
(4)还原:将用数学方法得到的结论,还原为实际问题的意义,并舍去不合题意的结论.
与函数有关的应用题,经常涉及物价、路程、产值、环保等实际问题,也可涉及角度、面积、体积、造价的最优化问题.主要类型有一次函数型、二次函数型、指数函数型和对数函数型等.在解决函数模型综合问题时,要认真分析、处理好各种关系,把握问题的主线,运用相关的知识和方法逐步化归为基本问题,尤其是要注意等价转换、分类讨论、数形结合思想的综合运用.其解题关键是确切建立相关函数解析式,然后应用函数、方程和不等式有关知识加以综合解答. | 





